Bühlmann model
The Bühlmann model (named after Hans Bühlmann) is a random effects model (or "variance components model" or hierarchical linear model) used in credibility theory in actuarial science to determine the appropriate premium for a group of insurance contracts.
A simplified form of the classical Bühlmann model where the components are assumed independent and the variances are equal for all observations, as well as the number of policies in each cell, is called the balanced Bühlmann model. In this model the claim statistics are determined by
where 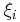 and
and 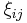 are independent random variables for which
are independent random variables for which
Here the interpretation of the random effects components is as follows:
-
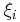 represents the departure of the true mean for all possible samples of members in group i from the overall mean m;
represents the departure of the true mean for all possible samples of members in group i from the overall mean m;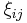 represents the departure of the j'th selected individual in group i from the true mean,
represents the departure of the j'th selected individual in group i from the true mean, 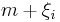 , for that group.
, for that group.
References
- Bühlmann, H. (1967) "Experience rating and credibility", ASTIN Bulletin 4, 199–207.
- Frees, E.W., Young, V.R., Luo, Y., (1999) "A longitudinal data analysis interpretation of credibility models", Insurance: Mathematics and Economics, 24 (3), 229–247. doi: 10.1016/S0167-6687(98)00055-9
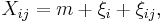
![\operatorname{E}[\xi_i]=\operatorname{E}[\xi_{ij}]=0, \operatorname{var}[\xi_i]=a, \operatorname{var}[\xi_{ij}]=s^2.](/2012-wikipedia_en_all_nopic_01_2012/I/fd7ab47a14b6f80109123212e1be192e.png)